Mittelsenkrechten mit Excel? (Kreisberechnung)

[Eastpak1984]

Hallo,

für einen Cache sind 3 Punkte gegeben, A, B, und C.
Nundenkt man sich einen Punkt X, um den ein Kreis verläuft, der A, B, C schneidet.

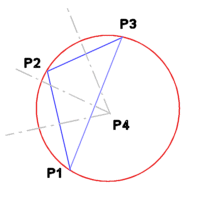
Quasi ein Umkreis eines Dreieckes... der müsste im Schnittpunkt der Mittelsenkrechten von den Strecken AB, BC und AC liegen.


Weiss jemand, wie man sowas mit Excel oder so berechnen könnte?

PS: Mit Papier war das kein Problem, doch sind die Punkte A, B, C sehr ungenau beschrieben (es sind keine Koord. genannt, sondern wirklich recht große Gebäude...)

 

[t31]

Rechnerisch wäre mir das zu aufwändig. Man kann natürlich Kreise und deren Schnittpunkte berechnen, sind alle Radien gleich, hast du den Punkt.
Ich selbst löse so etwas ganz pragmatisch mit Mapsource, die drei Punkte A, B, C eingeben und dann Radien per Annäherungsalarm zeichnen und so lange anpassen bis es passt. Dauert im Regelfall keine Minute.

 

[1887]

Weiss jemand, wie man sowas mit Excel oder so berechnen könnte?

PS: Mit Papier war das kein Problem, doch sind die Punkte A, B, C sehr ungenau beschrieben (es sind keine Koord. genannt, sondern wirklich recht große Gebäude...)

???

Mit sehr großen Gebäuden lassen sich keine konkreten Zielkoordinaten berechnen. Von irgendwo sollen doch sicher die Koordinaten bestimmt werden? Hat man diese, kann man den Radius bestimmen und mit dem Schnittpunkt der drei Annäherungskreise das Zentrum bestimmen.

Grüße
1887

 

[Eastpak1984]

Hm, ich zitiere mal den relevanten Part:

Schlage ich mit dem Zirkel einen Kreis um den Mittelpunkt eines Parkplatzes in der Nähe
des gesuchten Ortes, so kreuzt er drei wichtige Gebäude:

Gebäude 1: Es hat einen 61m hohen Turm und wurde am Ende des 19. Jahrhunderts errichtet.

Gebäude 2: Es steht auf dem Gelände des alten Kreuzklosters.

Gebäude 3: Es war am Anfang des 19. Jahrhunderts "Mittelpunkt des geistigen und
gesellschaftlichen Lebens"

Die Koordinaten des Parkplatzes sind N52 15.XXX E10 30.YYY

Die Quersumme von XXX ist 17.

Die Quersumme von YYY ist 21.


Aus BS - Stadtpiraten (GCHK9H)

 

[1887]

Moin,

na dann nimmt man die halbwegs in der Mitte der Gebäude liegenden Punkte, bestimmt die Entfernungen und berechnet Winkel und anschließend den Radius. So weiß man immerhin schon den Parkplatz.

Grüße
1887

 

[t31]

Naja groß helfen kann man da nicht, die Gebäude mußt du selbst finden, als nicht Braunschweiger bin ich da eh im Nachteil. Wenn du sie aber hast, dann ist das relativ schnell grafisch gelöst und so genau muß das nicht sein. Du weißt ja im jeden Falle, das es die Mitte eines Parkplatzes ist und die Quersumme hast du auch, so das auch die letzte Stelle sicher bestimmt werden kann.

 

[Eastpak1984]

Hm, ist das mit Excel also gar nicht sooo einfach? Schade

 

[Millhouse]

Mit einem Mopsos-Skript auf einem PDA ist das aber nicht schwer. Die Punkte kann man natürlich nur näherungsweise angeben. Die Lösung müsste einen aber trotzdem auf den Parkplatz führen. Dann kann man ja den Mittelpunkt des Parkplatzes "klassisch" mit GPS oder Karte bestimmen und mit der Quersumme feinjustieren.

program Mittelpunkt;
var
	Lat1,Lon1: real;
	Lat2,Lon2: real;
	Lat3,Lon3: real;
	Lat4,Lon4: real;  

begin
	Lat1:= 'N 51° 36.473';
	Lon1:= 'N 6° 39.585';
	
	Lat2:= 'N 51° 36.173';
	Lon2:= 'N 6° 40.821';
	
	Lat3:= 'N 51° 35.772';
	Lon3:= 'N 6° 40.787';

	circumcircle(Lat1,Lon1,Lat2,Lon2,Lat3,Lon3,Lat4,Lon4);
  	
  	writeln('Mittelpunkt : ',WGS84(Lat4,Lon4));
end.

Das ganze Geheimnis steckt natürlich in der Funktion circumcircle(). Aber das bedeutet, das das ganze numerisch lösbar ist!

Den zugrunde liegenden Algorithmus (Den ich leider nicht kenne, der aber nicht kompliziert zu sein scheint.) müsste man somit auch mit Excel nachbilden können.

PS: Der verwendete Mittelpunkt wäre exakt: N 51° 36.000 E 6° 40.000 .

 

[t31]

Mit Excel ging das schon, dazu müsste KDB dann den Algorithmus sponsern - würde mich auch interessieren - ABER, dann auch nur per VBA (eigene Funktionen schreiben), ansonsten würde man sich ganz sicher in den Excel-Tabellen verlieren.
Anderseits ist das grafisch schnell gemacht, warum dann rechnen?

 

[Eastpak1984]

Stichwort unterwegs? ;-)

Und nee, so schnell gehts in diesem Falle ja nicht...

 

[t31]

Unterwegs - sofern du keinen Oregon hast (sondern was richtig solides, Vista HCx oder ein GPSmap 60Cx) - kannst du ebenfalls, wenn auch nicht so komfortabel, mit dem Annäherungsalarm arbeiten. Dann allerdings nur mit 10m Genauigkeit.

 

[Eastpak1984]

Hab ich aber

 

[Schnueffler]

Schau Dir mal geogebra an. Damit kann man das relativ einfach berechnen. Du musst nur vorher die Koordinaten in UTM umrechnen.

 

[KoenigDickBauch]

Den zugrunde liegenden Algorithmus (Den ich leider nicht kenne, der aber nicht kompliziert zu sein scheint.) müsste man somit auch mit Excel nachbilden können.

CircumCircle berechnet einen Umkreis eines Dreieck das mit diesen Drei Punkten beschrieben wird.

Der Algorithmus kann auch in Excel gemacht werden. (Konvertieren nach GK (gleiche Zone beachten), Geradengleichungen der Mittelsenkrechten aufbauen, Geraden schneiden)