beef_productions
Geocacher
hallo,
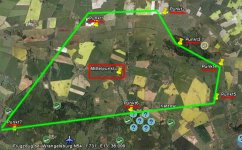
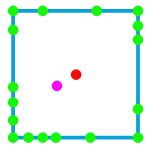
wir planen für das frühjahr einen kleinen wandermulti mit einer runde von 30 km. als bonus haben wir uns gedacht, wir nehmen genau den mittelpunkt der durch die route abgegrenzte fläche. wir haben jetzt schon eine komplette trackaufzeichnung von der route. wie kommt man jetzt von der durch die route eingeschlossene fläche auf den mittelpunkt davon? und das möglichst genau?
vielen dank für eure hilfe.
beef_productions
wir planen für das frühjahr einen kleinen wandermulti mit einer runde von 30 km. als bonus haben wir uns gedacht, wir nehmen genau den mittelpunkt der durch die route abgegrenzte fläche. wir haben jetzt schon eine komplette trackaufzeichnung von der route. wie kommt man jetzt von der durch die route eingeschlossene fläche auf den mittelpunkt davon? und das möglichst genau?
vielen dank für eure hilfe.
beef_productions